Juros Compostos: Como Calcular, Fórmula e Exemplos Práticos 2026

Os juros compostos representam um dos conceitos mais fundamentais do sistema financeiro moderno. Diferentemente dos juros simples, que incidem apenas sobre o capital inicial, os juros compostos acumulam-se período após período, gerando o que popularmente conhecemos como “juros sobre juros”. Este mecanismo de capitalização exponencial pode ser tanto o maior aliado de um investidor quanto o principal desafio de quem contrai dívidas.
Compreender como calcular juros compostos não é apenas uma questão de conhecimento teórico – é uma habilidade prática que impacta diretamente decisões financeiras cotidianas.
Desde a escolha de um investimento em renda fixa até a contratação de um financiamento veicular ou imobiliário, os juros compostos estão presentes, silenciosamente moldando o custo real de cada operação financeira.
A diferença entre dominar ou desconhecer este conceito pode representar milhares – ou até dezenas de milhares – de reais ao longo do tempo.
Um investimento de R$10 mil aplicado por 20 anos a 6% ao ano renderá R$22.071,00 em juros compostos, comparado a apenas R$12 mil em juros simples.
Por outro lado, um financiamento aparentemente acessível pode ocultar um custo total que supera em mais de 50% o valor original do bem adquirido.
Neste artigo, você encontrará uma abordagem completa e estruturada sobre juros compostos.
Apresentaremos a fórmula matemática e seu detalhamento, demonstraremos cálculos passo a passo, compararemos diferentes cenários através de tabelas comparativas e analisaremos exemplos práticos extraídos do mercado financeiro brasileiro.
Além disso, disponibilizaremos ferramentas gratuitas e confiáveis para realizar seus próprios cálculos, incluindo um tutorial detalhado de como criar planilhas no Excel.
Ao final desta leitura, você estará apto a calcular juros compostos com precisão, compreender seu impacto em investimentos e financiamentos, e tomar decisões financeiras substancialmente mais informadas e estratégicas.
O Que São Juros Compostos?
Juros compostos constituem um regime de capitalização no qual os rendimentos de cada período são incorporados ao capital, gerando novos rendimentos nos períodos subsequentes.
Em termos técnicos, trata-se de uma progressão geométrica onde a base de cálculo aumenta continuamente, diferindo fundamentalmente dos juros simples, que mantêm a base fixa durante todo o período.
O termo “juros sobre juros” descreve adequadamente este fenômeno: ao final de cada período de capitalização – seja ele diário, mensal ou anual – os juros gerados não são retirados, mas sim adicionados ao montante principal. Este novo total serve então como base para o cálculo dos juros do período seguinte, criando um efeito de acumulação exponencial.
Este sistema predomina na quase totalidade das operações financeiras contemporâneas.
Aplicações em renda fixa, financiamentos imobiliários, empréstimos pessoais, cartões de crédito e até mesmo a correção de débitos tributários utilizam juros compostos como mecanismo de cálculo. A prevalência deste modelo justifica-se pela sua capacidade de refletir mais fielmente o custo de oportunidade do capital ao longo do tempo.
Juros Simples vs Juros Compostos
A distinção entre estes dois regimes de capitalização manifesta-se claramente através de um exemplo numérico.
Considere um investimento inicial de R$1.000,00 submetido a uma taxa de 10% ao ano durante 3 anos:
Regime de Juros Simples
- Ano 1: R$1.000,00 + (R$1.000,00 × 10%) = R$1.100,00;
- Ano 2: R$1.100,00 + (R$ 1.000,00 × 10%) = R$1.200,00;
- Ano 3: R$1.200,00 + (R$ 1.000,00 × 10%) = R$1.300,00;
- Montante final: R$1.300,00 (crescimento de 30%).
Regime de Juros Compostos
- Ano 1: R$1.000,00 × 1,10 = R$1.100,00;
- Ano 2: R$1.100,00 × 1,10 = R$1.210,00;
- Ano 3: R$1.210,00 × 1,10 = R$1.331,00;
- Montante final: R$ 1.331 (crescimento de 33,1%).
A diferença de R$31,00 pode parecer modesta em um período de apenas três anos, mas esta disparidade amplifica-se exponencialmente conforme o tempo se estende.
A característica fundamental é que nos juros simples, o incremento anual permanece constante (R$100,00), enquanto nos juros compostos, o incremento aumenta progressivamente (R$100,00, depois R$110,00, depois R$121,00).
Nos juros simples, a taxa incide exclusivamente sobre o capital inicial durante toda a operação. Este modelo encontra aplicação primária em operações de curtíssimo prazo ou em contextos específicos definidos por legislação.
Já os juros compostos permitem que o capital trabalhe de forma mais eficiente, pois os rendimentos são continuamente reinvestidos, potencializando o efeito do tempo sobre o patrimônio.
O Efeito Exponencial dos Juros Compostos
A característica distintiva dos juros compostos reside em sua natureza exponencial.
Enquanto crescimentos lineares adicionam quantias constantes ao longo do tempo, crescimentos exponenciais multiplicam o capital por fatores que se acumulam progressivamente. Esta característica matemática transforma o tempo no fator mais determinante para o resultado final de qualquer operação financeira.
O impacto de longo prazo dos juros compostos torna-se evidente quando examinamos períodos superiores a uma década.
Um investimento que rende 10% ao ano em juros compostos não dobra em 10 anos – ele multiplica-se por 2,59 vezes.
Em 20 anos, não quadruplica: multiplica-se por 6,73 vezes.
Em 30 anos, atinge 17,45 vezes o valor inicial.
Esta progressão geométrica explica por que investidores de longo prazo enfatizam tanto a importância de começar cedo e manter consistência.
Por outro lado, esta mesma força matemática atua contra devedores.
Uma dívida sujeita a juros compostos elevados pode crescer de forma vertiginosa, tornando-se rapidamente impagável se não administrada adequadamente.
No mercado de crédito brasileiro, onde taxas mensais de cartão de crédito podem ultrapassar 10%, uma dívida pode dobrar em menos de um ano quando deixada sem controle.
A compreensão desta dinâmica é fundamental para qualquer planejamento financeiro sólido.
Os juros compostos não são intrinsecamente benéficos ou prejudiciais – são uma ferramenta matemática neutra que amplifica resultados ao longo do tempo. Utilizados conscientemente, potencializam a construção de patrimônio; ignorados ou mal compreendidos, podem comprometer décadas de trabalho em poucos anos de endividamento.
Como Calcular Juros Compostos: Fórmula e Passo a Passo
O cálculo de juros compostos fundamenta-se em uma expressão matemática elegante e precisa que captura a essência do crescimento exponencial:
M = C × (1 + i)^t
M = Montante final (capital + juros acumulados);
C = Capital inicial (valor principal investido ou emprestado);
i = Taxa de juros por período (expressa em decimal);
t = Número de períodos de capitalização.
Esta fórmula deriva diretamente da progressão geométrica e representa a aplicação sucessiva da taxa de juros sobre um capital que se renova a cada período.
A potência (1 + i)^t constitui o fator de capitalização, responsável pela característica exponencial do crescimento.
Para calcular apenas o valor dos juros acumulados, sem o capital inicial, utiliza-se:
J = M – C
Ou, expandindo:
J = C × [(1 + i)^t – 1]
É fundamental compreender que a taxa i e o tempo t devem estar expressos na mesma unidade temporal. Se a taxa é mensal, o tempo deve ser em meses; se a taxa é anual, o tempo deve ser em anos.
A incompatibilidade entre estas unidades constitui um dos erros mais frequentes em cálculos financeiros.
Entendendo Cada Variável da Fórmula
Capital Inicial (C)
O capital inicial representa o valor sobre o qual os juros começam a incidir. Em contextos de investimento, corresponde ao montante aplicado no momento inicial.
Em operações de crédito, representa o valor efetivamente recebido pelo mutuário. Este valor deve ser líquido de taxas administrativas ou outros encargos que não sejam os próprios juros.
Para operações que envolvem aportes periódicos adicionais, a fórmula básica requer adaptações.
Cada novo aporte constitui, tecnicamente, um novo capital inicial com seu próprio tempo de aplicação, demandando cálculos individualizados ou o uso de fórmulas específicas para séries de pagamentos.
Taxa de Juros (i)
A taxa de juros expressa o percentual de remuneração ou custo do capital por período.
Sua conversão de percentual para decimal é obrigatória para aplicação na fórmula: uma taxa de 2% torna-se 0,02; uma taxa de 12% torna-se 0,12.
É crucial distinguir entre diferentes formas de expressão da taxa:
- Taxa nominal: declarada no contrato, geralmente em termos anuais;
- Taxa efetiva: taxa realmente praticada no período de capitalização;
- Taxa proporcional: obtida por divisão simples (ex: taxa anual ÷ 12 para mensal);
- Taxa equivalente: produz o mesmo resultado ao final de um período, considerando capitalização composta.
A taxa proporcional difere matematicamente da taxa equivalente.
Para converter uma taxa anual em mensal usando juros compostos, a fórmula correta é:
i_mensal = (1 + i_anual)^(1/12) – 1
Exemplo: uma taxa de 12% ao ano não equivale a 1% ao mês em juros compostos. A taxa mensal equivalente é:
- i_mensal = (1,12)^(1/12) – 1 = 0,009489 ou 0,9489% ao mês.
Tempo (t)
O tempo representa o número de períodos durante os quais os juros serão capitalizados. Sua unidade deve coincidir com a da taxa de juros. Em operações financeiras típicas:
- Investimentos em renda fixa: geralmente expressos em dias corridos;
- Financiamentos: usualmente em meses;
- Análises de longo prazo: frequentemente em anos.
Para períodos fracionários, a fórmula aceita valores decimais.
Um investimento de 2 anos e 6 meses equivale a t = 2,5 anos, desde que a taxa também seja anual.
Montante Final (M)
O montante representa o valor total ao final da operação, incluindo o capital inicial e todos os juros acumulados. É o resultado da aplicação da fórmula e constitui a informação mais relevante para tomada de decisão em investimentos (quanto se receberá) ou financiamentos (quanto se pagará).
Passo a Passo do Cálculo
Para exemplificar a aplicação prática da fórmula, considere o seguinte cenário:
Situação: você investe R$10.000,00 em um CDB que rende 1% ao mês, mantendo o investimento por 12 meses.
Passo 1: Identificar as variáveis
- C = R$ 10.000,00;
- i = 1% ao mês = 0,01 (em decimal);
- t = 12 meses.
Passo 2: Verificar compatibilidade
- Taxa: mensal;
- Tempo: meses;
- Compatibilidade confirmada ✓
Passo 3: Aplicar a fórmula
- M = C × (1 + i)^t;
- M = 10.000 × (1 + 0,01)^12;
- M = 10.000 × (1,01)^12.
Passo 4: Calcular a potência
- (1,01)^12 = 1,126825.
Passo 5: Multiplicar pelo capital
- M = 10.000 × 1,126825;
M = 11.268,25.
Passo 6: Calcular os juros
- J = M – C;
- J = 11.268,25 – 10.000,00;
- J = 1.268,25.
Interpretação do Resultado
Ao final de 12 meses, seu investimento inicial de R$10.000,00 terá se transformado em R$11.268,25, representando um ganho de R$1.268,25 em juros.
O retorno total é de 12,68%, superior aos 12% que se obteria pela simples multiplicação da taxa mensal (1% × 12), evidenciando o efeito da capitalização composta.
Se este mesmo investimento fosse mantido por 24 meses (M = 10.000 × (1,01)^24 = R$12.697,35), os juros acumulados seriam de R$ 2.697,35, demonstrando que no segundo ano, você ganhou R$ 1.429,10 – mais do que no primeiro ano (R$1.268,25), precisamente devido ao efeito dos juros compostos.
Análise Comparativa: O Impacto dos Juros Compostos
Para compreender de forma tangível como os juros compostos se comportam sob diferentes condições, apresentamos uma análise comparativa sistemática.
Utilizando um capital inicial padrão de R$10.000,00, examinaremos cinco cenários distintos que variam em taxa de juros e prazo de aplicação, sempre comparando os resultados obtidos por juros simples e juros compostos.
Tabela Mestre: Comparação entre Regimes de Capitalização
Capital Inicial: R$10.000,00
| Cenário | Descrição | Taxa a.a. | Prazo | Juros Simples | Juros Compostos | Vantagem Compostos |
| A | Conservador – Curto Prazo | 6% | 5 anos | R$13.000,00 | R$13.382,26 | +2,9% |
| B | Conservador – Médio Prazo | 6% | 10 anos | R$16.000,00 | R$17.908,48 | +11,9% |
| C | Conservador – Longo Prazo | 6% | 20 anos | R$22.000,00 | R$32.071,35 | +45,8% |
| D | Moderado – Médio Prazo | 10% | 10 anos | R$20.000,00 | R$25.937,42 | +29,7% |
| E | Agressivo – Médio Prazo | 12% | 10 anos | R$22.000,00 | R$31.058,48 | +41,2% |
Análise Detalhada dos Juros Acumulados
Para compreender não apenas o montante final, mas especificamente quanto foi gerado em juros, a tabela seguinte isola estes valores:
| Cenário | Juros Simples | Juros Compostos | Diferença Absoluta | Crescimento sobre Capital |
| A | R$3.000,00 | R$3.382,26 | R$382,26 | +33,8% vs +30,0% |
| B | R$6.000,00 | R$7.908,48 | R$1.908,48 | +79,1% vs +60,0% |
| C | R$12.000,00 | R$22.071,35 | R$10.071,35 | +220,7% vs +120,0% |
| D | R$10.000,00 | R$15.937,42 | R$5.937,42 | +159,4% vs +100,0% |
| E | R$12.000,00 | R$21.058,48 | R$9.058,48 | +210,6% vs +120,0% |
Interpretação dos Resultados
O Efeito Exponencial do Tempo (Cenários A → B → C)
A progressão dos cenários A, B e C mantém constante a taxa de 6% ao ano, alterando apenas o prazo. Esta estrutura permite isolar o efeito do tempo sobre o crescimento do capital:
Em 5 anos (Cenário A), a vantagem dos juros compostos manifesta-se de forma discreta: R$ 382,26 adicionais, representando 2,9% a mais que os juros simples. O capital cresce 33,8% em vez de 30,0%.
Em 10 anos (Cenário B), o efeito exponencial começa a se evidenciar claramente. A diferença salta para R$ 1.908,48 – cinco vezes superior ao observado em 5 anos, embora o tempo tenha apenas dobrado. A vantagem percentual eleva-se para 11,9%.
Em 20 anos (Cenário C), o crescimento exponencial revela sua verdadeira magnitude. Os juros compostos geram R$10.071,35 a mais que os juros simples – uma diferença superior ao próprio capital inicial. Enquanto os juros simples proporcionam retorno de 120%, os juros compostos entregam 220,7%, uma diferença de 100,7 pontos percentuais.
Esta progressão não é linear: a vantagem não dobra quando o tempo dobra. Ela se amplifica exponencialmente, confirmando matematicamente que o tempo constitui o fator mais influente em operações com juros compostos.
Juros Compostos e Inflação: Taxa Real vs. Taxa Nominal
A análise de operações financeiras sujeitas a juros compostos torna-se incompleta quando não considera o efeito da inflação sobre o poder aquisitivo.
A distinção entre taxa nominal e taxa real constitui aspecto fundamental para avaliação adequada de investimentos e financiamentos, especialmente em economias com histórico inflacionário significativo como a brasileira.
Taxa Nominal e Taxa Real: Conceitos Fundamentais
Taxa Nominal representa o percentual de juros declarado em contratos financeiros, sem ajuste pelo efeito da inflação. É o valor que aparece em certificados de investimento, propostas de financiamento e extratos bancários.
Taxa Real expressa o ganho ou custo efetivo em termos de poder aquisitivo. Ela responde à questão fundamental: quanto realmente ganhei (ou paguei) considerando que os preços na economia também aumentaram?
O economista Irving Fisher desenvolveu a expressão matemática que relaciona estas três variáveis:
(1 + i_nominal) = (1 + i_real) × (1 + inflação)
Rearranjando para isolar a taxa real:
i_real = [(1 + i_nominal) / (1 + inflação)] – 1
Exemplo Prático:
Um investimento oferece retorno nominal de 12% ao ano em um período com inflação de 6% ao ano:
- i_real = [(1,12) / (1,06)] – 1;
- i_real = 1,056604 – 1;
- i_real = 5,66% ao ano.
O retorno real de 5,66% ao ano significa que, descontado o efeito inflacionário, o poder aquisitivo do investidor aumentou em 5,66%. Esta é a medida verdadeira de criação de riqueza.
Impacto da Inflação em Investimentos
Para investidores, a taxa real determina se existe criação efetiva de riqueza. Considere três cenários com investimento inicial de R$ 50.000,00 por 5 anos:
| Cenário | Taxa Nominal | Inflação | Taxa Real | Montante Nominal | Poder Aquisitivo | Resultado |
| 1 | 10% a.a. | 4% a.a. | 5,77% a.a. | R$80.525,50 | R$66.234,71 | Ganho real de R$16.234,71 |
| 2 | 4% a.a. | 4% a.a. | 0% a.a. | R$60.832,65 | R$50.000,00 | Preservação de capital |
| 3 | 6% a.a. | 8% a.a. | -1,85% a.a. | R$66.911,28 | R$45.579,57 | Perda real de R$4.420,43 |
O Cenário 3 ilustra situação frequentemente mal compreendida: o investidor vê seu saldo crescer nominalmente, mas seu patrimônio real diminui.
Esta dinâmica explica por que investimentos em caderneta de poupança podem resultar em perda patrimonial em períodos de inflação elevada.
Impacto da Inflação em Financiamentos
Para operações de crédito, a inflação atua em favor do devedor, reduzindo o custo real do financiamento.
Um financiamento contratado a 8% ao ano nominal, em período de inflação de 6% ao ano, tem custo real de: i_real = [(1,08)/(1,06)] – 1 = 1,89% ao ano.
Exemplo: Financiamento Imobiliário
- Valor: R$300.000,00;
- Taxa nominal: 9% ao ano;
- Prazo: 20 anos (Sistema Price);
- Parcela mensal: R$2.699,62;
- Inflação média projetada: 4% ao ano.
Custo real efetivo: taxa real = [(1,09)/(1,04)] – 1 = 4,81% ao ano.
O custo real do financiamento é 4,81% ao ano, não 9%.
As parcelas de R$ 2.699,62 comprometem cada vez menos do orçamento em termos reais, pois a renda nominal tende a acompanhar a inflação enquanto a parcela permanece fixa.
Evolução do poder aquisitivo da parcela:
| Ano | Parcela Nominal | Poder Aquisitivo (valores do ano 1) |
| 1 | R$2.699,62 | R$2.699,62 |
| 10 | R$2.699,62 | R$1.823,27 |
| 20 | R$2.699,62 | R$1.233,79 |
No último ano, a parcela terá poder aquisitivo equivalente a apenas 45,7% do valor inicial, beneficiando significativamente o devedor.
Esta dinâmica explica por que financiamentos de longo prazo em economias com inflação moderada podem ser estrategicamente vantajosos.
Decisões Financeiras Baseadas em Taxa Real
Para Investimentos
Ao avaliar duas opções – renda fixa pós-fixada (100% CDI = 11,25% a.a.) versus pré-fixada (12% a.a.) – com inflação projetada de 4,5% a.a.:
- Taxa real pós-fixada: 6,46% ao ano;
- Taxa real pré-fixada: 7,18% ao ano.
A opção pré oferece 0,72 pontos percentuais adicionais em termos reais.
Contudo, a pós protege contra surpresas inflacionárias acima da projeção, enquanto a pré garante retorno fixo apenas se a inflação não superar significativamente 4,5%.
Para Financiamentos
Entre financiamento pré-fixado (9% a.a.) e pós-fixado (5% a.a. + IPCA), com inflação projetada de 4% a.a.:
- Pré: custo real de 4,81% ao ano (varia com inflação);
- Pós: custo real fixo de 5% ao ano (independente da inflação).
O pós mantém custo real constante, transferindo risco inflacionário ao mutuário. O pré tem custo real que varia inversamente: se inflação subir, custo real cai; se cair, custo real sobe.
Planejamento de Longo Prazo
Em horizontes superiores a 10 anos, inflação acumulada de 4% ao ano reduz o poder aquisitivo para 67,6% em 10 anos, 45,6% em 20 anos, e 30,8% em 30 anos.
Por isso, metas de aposentadoria devem ser expressas em valores reais ou múltiplos do custo de vida esperado no futuro.
Um planejamento que vise renda mensal de R$10.000,00 daqui a 30 anos deve acumular capital suficiente para gerar aproximadamente R$32.434,00 nominais, considerando essa inflação.
Calculadoras de Juros Compostos: Ferramentas Gratuitas e Confiáveis
Embora a compreensão da fórmula matemática seja fundamental, a utilização de calculadoras digitais agiliza consideravelmente a análise de cenários financeiros complexos.
Estas ferramentas permitem testar rapidamente múltiplas hipóteses, comparar alternativas e visualizar projeções de longo prazo.
A escolha de calculadoras confiáveis, desenvolvidas por instituições respeitáveis, garante precisão nos resultados e segurança nas decisões.
Calculadora do Cidadão – Banco Central do Brasil
A Calculadora do Cidadão constitui a ferramenta oficial do Banco Central do Brasil para cálculos financeiros diversos. Sua credibilidade deriva da fonte institucional, metodologia transparente e ausência de interesses comerciais.
A ferramenta está disponível gratuitamente em: https://www3.bcb.gov.br/CALCIDADAO/
Funcionalidades Principais
A plataforma oferece diversos módulos de cálculo:
- Valor Futuro de um Capital: calcula o montante final de um investimento único;
- Aplicação com Depósitos Regulares: permite calcular o resultado de investimentos com aportes mensais;
- Financiamento com Prestações Fixas: calcula parcelas, prazos ou taxas pelo Sistema Price;
- Correção de Valores: atualiza valores históricos por diversos índices oficiais (IPCA, IGP-M, CDI, Selic, TR).
Para calcular o montante futuro de um investimento de R$10.000,00 a 1% ao mês por 12 meses, acesse o módulo “Valor Futuro de um Capital”, informe o valor do capital, a taxa de juros mensal e o número de meses, deixando o campo “Valor futuro” em branco.
Ao clicar em “Calcular”, o sistema retornará R$11.268,25 como montante final.
A ferramenta também está disponível como aplicativo para iOS e Android.
Calculadora de Juros Compostos – Mobills
A plataforma Mobills, especializada em educação financeira, oferece uma calculadora de juros compostos com interface moderna e recursos de visualização.
Disponível em: https://www.mobills.com.br/calculadoras/calculadora-juros-compostos/
Principais Diferenciais
A calculadora Mobills destaca-se pela interface intuitiva e recursos visuais: gera automaticamente gráficos de evolução do investimento, apresenta tabela detalhada mês a mês com decomposição de saldos e juros, permite exportação dos resultados em Excel ou CSV, e integra nativamente o cálculo com aportes periódicos.
Para simular um investimento de R$10.000,00 iniciais com aportes mensais de R$500,00, a 1% ao mês por 24 meses, basta preencher os campos correspondentes e clicar em “Calcular”.
O sistema exibirá que o valor total investido será de R$22.000,00, gerando R$3.087,28 em juros, totalizando R$25.087,28.
Comparação e Recomendações de Uso
| Aspecto | Banco Central | Mobills |
| Credibilidade | Máxima (órgão oficial) | Alta (empresa estabelecida) |
| Interface | Básica/funcional | Moderna/intuitiva |
| Visualização gráfica | Não | Sim |
| Exportação de dados | Não | Sim (Excel/CSV) |
| Correção por índices oficiais | Sim | Não |
| Cálculo de financiamentos | Sim | Não |
| Aplicativo mobile | Sim | Não |
Para validação oficial e correção monetária, utilize a Calculadora do Banco Central, especialmente quando precisar de índices históricos oficiais ou cálculos com implicações contratuais.
Para análise exploratória e apresentações visuais, utilize a calculadora Mobills, que oferece recursos gráficos e permite testar rapidamente múltiplos cenários.
Idealmente, para decisões financeiras importantes, recomenda-se utilizar ambas as ferramentas para validação cruzada dos resultados.
Independente da ferramenta escolhida, sempre verifique se taxas e prazos estão na mesma unidade temporal e confirme a razoabilidade dos resultados.
Como Calcular Juros Compostos no Excel
O Microsoft Excel constitui ferramenta amplamente disponível e extremamente versátil para cálculos de juros compostos.
Método Básico: Fórmula Direta
Este método aplica diretamente a fórmula matemática.
| Célula | Conteúdo | Valor |
| B1 | Capital Inicial | 10000 |
| B2 | Taxa (decimal) | 0,01 |
| B3 | Períodos | 12 |
| B4 | =B1*(1+B2)^B3 | 11268,25 |
Método Avançado: Tabela Mês a Mês
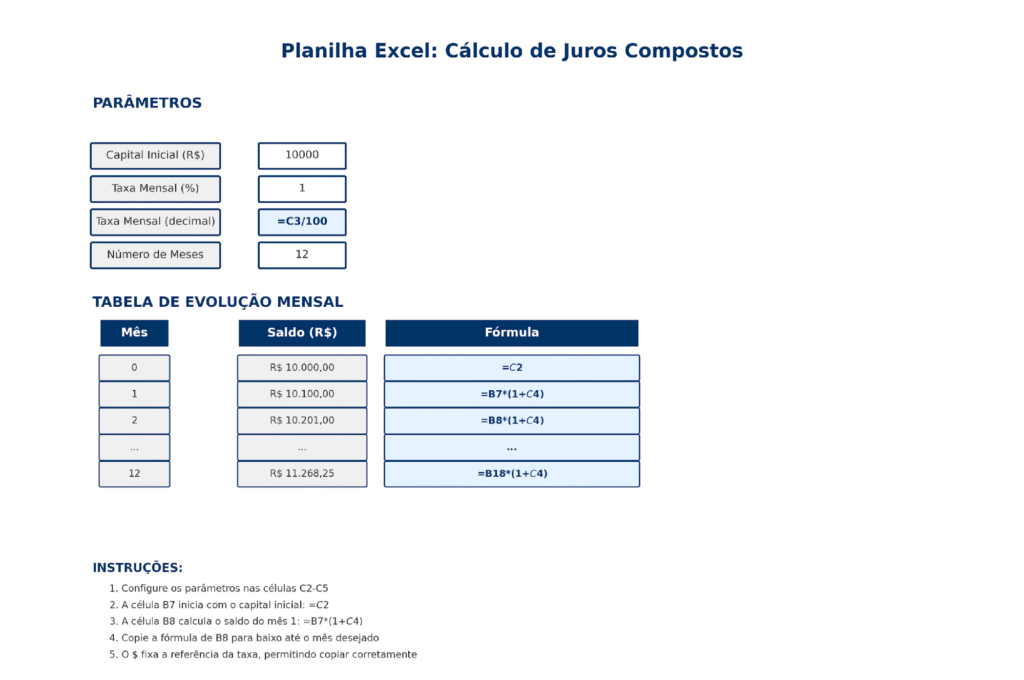
Construção:
- B7: =$C$2;
- 2. B8: =B7*(1+$C$4);
- 3. Copie B8 para baixo.
Aplicações Práticas
Financiamento de Veículo
Cenário: veículo de R$ 50.000 em 48 meses. Três propostas:
| Cenário | Taxa | Parcela | Total | Juros | Custo |
| 1 – Concessionária | 1,89% | R$1.593,82 | R$76.503,00 | R$26.503,00 | 53% |
| 2 – Banco Trad. | 1,50% | R$1.468,75 | R$70.500,00 | R$20.500,00 | 41% |
| 3 – Banco Digital | 1,19% | R$1.373,36 | R$65.921,00 | R$15.921,00 | 32% |
Diferença de 0,70 p.p. representa economia de R$10.582,00.
Dívida de Cartão de Crédito
Dívida de R$5.000,00 a 10% a.m.:
| Período | Saldo |
| Início | R$5.000,00 |
| 6 meses | R$8.858,00 |
| 12 meses | R$15.692,00 |
Taxa efetiva anual: 213,84%. Priorize pagamento total da fatura.
Conversão de Taxas
Método correto: i_mensal = (1 + i_anual)^(1/12) – 1. Exemplo: 12% a.a. = 0,9489% a.m.
Estratégias de Otimização
Investimentos:
- Iniciar cedo;
- Aportes regulares;
- Reinvestir rendimentos.
Financiamentos:
- Comparar taxas;
- Maximizar entrada;
- Evitar atrasos.
Perguntas Frequentes
Diferença simples vs compostos?
Simples incide só no capital. Compostos geram juros sobre juros.
Como calcular?
M = C × (1 + i)^t
Melhor calculadora?
Banco Central (bcb.gov.br/calcidadao) e Mobills.
Tempo para dobrar?
Regra de 72: 72 ÷ taxa. A 6% a.a. leva 12 anos.
Conclusão
Os juros compostos constituem mecanismo fundamental do sistema financeiro.
Este artigo apresentou a fórmula M = C × (1 + i)^t, aplicações práticas e ferramentas necessárias.
Pequenas diferenças em taxas amplificam-se exponencialmente.
R$10.000,00 a 6% por 20 anos gera R$32.071,00 (compostos) vs R$22.000,00 (simples) – 45,8% a mais.
Um financiamento com taxa 0,39 p.p. inferior economiza R$6.000,00.
O domínio deste conhecimento transforma-se em vantagem concreta: investidores maximizam retornos; mutuários minimizam custos.
O tempo é o fator mais determinante para construção ou destruição patrimonial.
Maurício Lindenmeyer Barbieri
Sócio da Barbieri Advogados
Mestre em Direito pela UFRGS
OAB/RS 36.798 | OAB/DF 24.037 | OAB/SC 61.179-A | OAB/PR 101.305 | OAB/SP 521.298
OAB Lisboa 64443L | RAK Stuttgart 50.159
Equipe de Redação da Barbieri Advogados é responsável pela produção e revisão de conteúdos técnicos, assegurando comunicação clara, precisa e alinhada aos valores institucionais. A Barbieri é inscrita na OAB/RS sob o nº 516.
E-mail: contato@barbieriadvogados.com
